Hola a [email protected] de nuevo, abro este hilo que viene de :
http://citroen.mforos.com/1257918/9[....]-pastillas-traseras/?pag=2#99846008
para no interferir con el del cambio de las pastillas de freno traseras por las que ha salido este debate de "pura física".
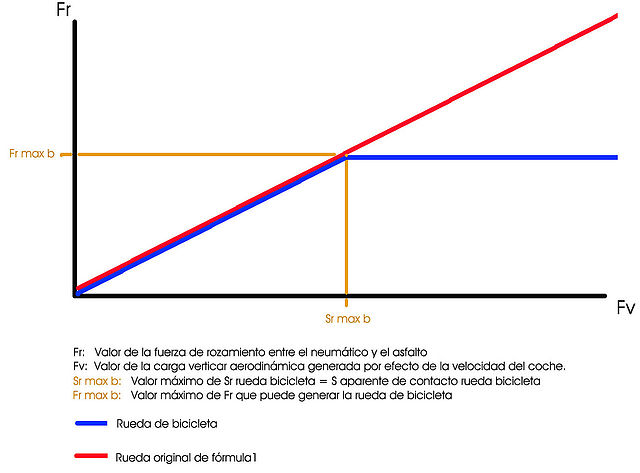
Recuerdo a [email protected] que estamos tratando de explicar por qué las pastillas ¿cuanto más superficie mejor? ó ¿porqué los fórmula 1 NO usan ruedas de bicicleta? :-)
Las leyes fundamentales de la fricción son:
1.- La fuerza de fricción es : F = u · N
2.- El coeficiente de rozamiento depende de los materiales que "rozan" y es independiente de la velocidad de deslizamiento. Esto es una aproximación teórica dado que
en la realidad los materiales modifican sus "condiciones" principalmente por temperatura.
tigre-est dices que F de rozamiento es independiente de la Superficie de Contacto (gran verdad) y luego dices que Fr no podrá seguir aumentando porque no habrá más
superficie de contacto disponible, y por mucho que aumente la carga aerodinámica el coche agarrará lo mismo a gran velocidad que a menor velocidad.
En ¿qué quedamos? ¿depende de la superficie Si ó No? ¿qué está pasando aquí? ¿cuanto más superficie mejor?¿porqué los fórmula 1 NO usan ruedas de bicicleta?
¿Falla lo que nos contaron de "pequeñitos" en Física? ¿Los "profes" eran unos mentirosos?
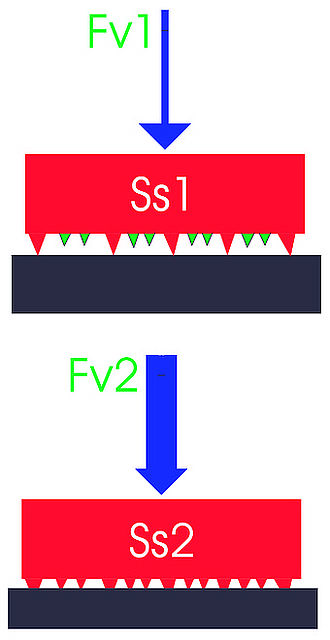
La clave a todo esto la ha dado el "maestro" tigre-est cuando decía que "... a escala microscópica, las superficies de los sólidos presentan cimas y valles, que podemos
evaluar midiendo su rugosidad. Debido a esta rugosidad, cuando dos superficies entran en contacto, no lo hacen en toda la superficie aparente de contacto (S), sino que
el contacto se verificará sólo en algunos puntos de estas rugosidades. A la suma de las áreas de los puntos en los que se verifica el contacto, la denominaremos área
real de contacto (Sr), y este área es independiente del área aparente de contacto (S). Estos puntos de contacto real son los encargados de soportar la carga normal (F)
que ejerce el pistón sobre la pastilla, y de generar la fuerza de fricción o fuerza de rozamiento (Fr). Cuando F aumenta, el número de puntos en contacto real aumenta,
aumentando el área real de contacto (Sr) a pesar de mantenerse invariable el área aparente (S). Como resultado, hemos de despreciar S y referirnos únicamente a Sr.
Así, la superficie real de contacto (Sr) queda contemplada ya en la potencia de (F x u), es decir, Fr aumenta en función de lo que aumente F, matizado por la naturaleza
de los materiales que estén en contacto, es decir, por el coeficiente de rozamiento (u)...."
La clave de todo esto está en ¿CUÁNDO SE DESTRUYE EL MATERIAL?. (u) es "constante" mientras NO haya destrucción de esas montañas, quiero decir:
1.- Hay una F de rozamiento "máxima" por unidad de superficie para cada material. UNA PRESIÓN MÁXIMA en la que (u) desfallece.
2.- A partir de esa Fr por unidad de superficie, el material (las montañas de cada material) se rompen, bajando el (u) coeficiente de rozamiento una barbaridad. Por esto se hacen los sistemas ABS.
3.- La clave está en la "densidad de fuerza"/presión máxima para la destrucción de los materiales y que está definida para cada material.
Esto quiere decir que a mayor SUPERFICIE de pastilla, MEJOR frenada máxima seremos capaces de realizar ó más fuerza del pie soportará la pastilla SIN
DESTRUIRSE la misma, es decir, SIN que (u) "desfallezca".
Lo que estoy tratando de decir con todo esto, es que da igual la superficie de contacto mientras NO haya destrucción de material (u) se mantiene pero existe una presión máxima y definida que hace que (u) baje su valor una barbaridad (rotura de las montañas) 
No se si mal comparado, pero es algo así como que si (en una tabla con clavos) tratas de doblar un único clavo/montaña, se dobla/rompe "fácil" pero si la tabla tiene
"muchos clavos/montañas" (mucha superficie) estas repartiendo el esfuerzo entre todos y se puede llegar a mucho mayor esfuerzo sin destrucción.
Lo que es constante y depende del material es la fuerza necesaria para "romper" una única montaña/clavo, es decir, la PRESIÓN que se puede ejercer sobre cada
material SIN romperlo.
Para mí hay una "densidad máxima de fuerza"/presión máxima para la destrucción de los materiales y que está definida y constante para cada material.
RESUMIENDO este "rollo":
1.- LA SUPERFICIE SI INTERVIENE PARA QUE LA FUERZA DE ROZAMIENTO MÁXIMA QUE SE PUEDE EJERCER SOBRE UNA PASTILLA/SUPERFICIE AUMENTE SIN DESTRUIR LA SUPERFICIE DE CONTACTO. (u) se mantenga constante.
2.- LA FUERZA QUE DESTRUYA LA SUPERFICIE DE CONTACTO SEA MAYOR.
Fijaros que curiosamente estamos diciendo que un Fórmula1 con ruedas de bicicleta pasa por curva a la misma velocidad que con el ancho habitual de ruedas SIEMPRE
Y CUANDO LA GOMA SEA DEL MISMO TIPO Y NO SE DESTRUYA.
Los fórmula 1 NO usan ruedas de bicicleta porque las romperían (me he quedado calvo), JAJAJAJAJA, porque sobrepasan la presión (Nw/m2) que soporta la goma SIN
romperse. SI NO SE ROMPIESE LA GOMA, SI DARÍA IGUAL Y USARÍAN RUEDAS DE BICICLETA. (Sobre todo porque serían más aerodinámicas) 
3.- A MAYOR SUPERFICIE DE PASTILLA, MEJOR FRENARÁ EL COCHE, PORQUE MÁS FUERZA PODRÁ HACER EL SERVO CONTRA LA PASTILLA SIN
ROMPERSE LA SUPERFICIE DE CONTACTO. (SIN bajar u).
4.- Presión de rotura de un material = constante del material = Pm = Presión máxima en la que u BAJA.
5.- Fuerza de rozamiento = N x u = P x S x u ==> N = P·S
N: fuerza de servos
u: coeficiente de rozamiento (que principalmente depende de Presión máxima/rotura)
P: presión=Fuerza ejercida sobre la pastilla por unidad de superficie.
S: Superficie de pastilla
Este tema me está gustando una barbaridad porque me ha hecho reflexionar "muchísimo" sobre algo tan aparentemente simple como era F=u·N y que lo ha hecho apasionante.
Creo que además debo pedir perdón por el "ladrillo". Alguno pensará ¡Vaya ROLLO!. No pasa nada , a otro tema y resuelto. 


Un saludo a [email protected],